Design Of Reinforced Concrete Beam as per ACI 318m Code

Nowadays, structure analysis and design are performed by using software. In the software, we analyze and design the structure as a frame instead of a separate structural element (i.e. slab, beam, and column), and, get the most accurate result in the minimum time. However, to interpret the design result, a designer must have a complete know-how of the design of each element (i.e. slabs, beam, column, and foundation) separately.

In the previous articles, I covered the basis of the design of slab and footing. In this article, I am discussing the basis of the design of the beam (i.e. flexural element). Hope it will be helpful for beginners.

The structure design of the reinforced Concrete beam is discussed below:

Contents

Minimum Depth of the Beam

First, determine the minimum depth of the beam as per the minimum depth specified in the ACI code (Refer to Table 1):

Support condition	Minimum Depth
Simply supported	L/16
For one end continuous	L/18.5
For two-end continuous	L/21
Cantilever	L/8

Table 1: Minimum depth of Beam as per ACI code

Applied Loads on the Beam

Dead Loads

Self-weight of beam
- Self-weight of beam in KN/m = unit wt of concrete × width of the beam × height of the beam.
Slab dead load
- Slab dead load (i.e. self wt of slab, finishes, etc.) is transferred as a dead load on the beam

If slab is one way;

Slab dead loads transferred on Longer beams in KN/m = Slab dead load (KN/m²) * Lx / 2

Slab dead loads transferred on shorter beams in KN/m= 0

If slab is two way;

Maximum Slab dead loads transferred on Longer beams in KN/m = Slab dead load (KN/m²)*Lx/6 *((3-(Lx/Ly)^2)

Maximum Slab dead loads transferred on Shorter beams in KN/m = Slab dead load (KN/m²) * Lx / 3

Here;

Ly is the longer dimension of slab

Lx is the shorter dimension of slab

Note: you can use the calculator available at this link”https://knowledgesharingplatform.com/load-distribution-from-slab-to-beam/”

Wall load.

Wall weight in KN/m = unit wt of material × thickness of wall × height of wall

For wall load calculation, you can use the calculator available at “https://knowledgesharingplatform.com/calculate-wall-weight-in-kn-m-kg-m-lb-ft/”

Live Load

Slab live load transferred on longer beams and shorter beams will be calculated as explained under the heading “slab dead load”.

Lateral Loads and Moments

Lateral load and moments due to lateral force are applied on a beam due to frame action, these loads and moments are generated due to the following:

seismic
Wind
Equipment or piping loads

Note: calculation of these lateral forces and moments will be covered in a separate blog

Miscellaneous Others Load (if applicable)

Following others, load (concentrated or uniformly) will be calculated and applied on a beam (if applicable) according to their nature (dead or live ):

OHWT weight
Any equipment weight
Cantilever slab reaction
Pipe and cable support
Platform load

Ultimate Loads on the Beam

Calculate ultimate loads (W_u) for the ultimate load combination specified by ACI 318M or any other applicable codes & standards.

Ultimate Forces and Moments

Maximum Shear (at a distance d from the face of Support)
Maximum negative moment (Hogging)
Maximum positive moment (Sagging)
Points of contra flexure(i.e. required for reinforcement curtailment)
Draw critical sections, for reinforcement optimization (For example, this 4m long beam has 3 critical sections due to a change in the value of both support moments)

However, you can also cover this design in two sections, by providing the same reinforcement at both ends.

Check Beam section is Singly Reinforced or Doubly Reinforced

Pickup the highest value of ultimate moment M_umax either bottom (+ve) moment or top(-ve) moment
Calculate Ru_max

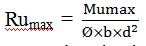
Here; = strength reduction factor taken as 0.9 for flexure

Calculate ρ

Calculate ρ_b

Calculate ρ_max= 0.634ρb for fy=416Mpa
If ρ < ρ_maxOK, the section will be designed as singly reinforced and there is no requirement for compression reinforcement.
If ρ > ρ_max, change the cross-section of the beam, especially increase the depth of the beam(if possible), so, that ρ < ρmax and the beam can be designed as singly reinforced, otherwise, design the beam as doubly reinforced (i.e. section having compression reinforcement). The design of a doubly Reinforced beam will be covered in the upcoming blog; whereas, it is not a cost-effective method.

Design of Singly Reinforced Section

Flexure Design

Calculate Ru for negative (-ve) moments and positive (+ve) moments of each critical section

Here; = strength reduction factor taken as 0.9 for flexure

Calculate ρ_required for both the top and bottom of each section using the below formula

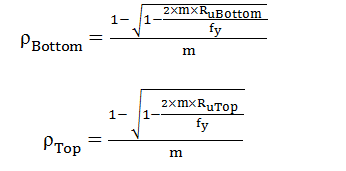
Calculate ρ_min of each section using below mentioned formula:

ρ_{min2 =}1.33ρ_required(i.e. ρ_Bottom or ρ_Top)

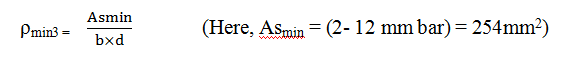
ρ_min= Maximum of (minimum(ρ_min1,ρ_min2),ρ_min3)

Check ρ_Bottomor ρ_Top of each section > ρ_min, otherwise, take ρ_Bottom& ρ_Top= ρ
Calculate the area of steel at bottom = max (ρ_Bottom, ρ_min)×b×d
Calculate the area of steel at the top = ρ_min×b×d
Calculate extra steel at top support = (ρ_{Top –}ρ_min ) × b ×d

you can also use the calculator for reinforcement calculation, which is available on this link “https://knowledgesharingplatform.com/flexural-reinforcement-calculator-as-per-code-aci-318m/”

Shear Design

Pick up maximum ultimate shear Vu from the beam analysis result
Calculate ØVc =

Calculate ØVc/ 2
If Vu < ØVc / 2, there is no need to provide shear reinforcement.
If ØVc / 2 < Vu < ØVc , means Vs = 0 only minimum shear reinforcement is required, Shear reinforcement spacing is calculated from the below formula ;