In this article, we will focus on the solution of systems of two linear equations. However, first understand what the linear equation in two variables is.
An equation is said to be a linear equation in two variables if it is written in the below form
ax + by + c=0
Here;
“x” and “y” are two variables, “a” and “b” are coefficients of x & y respectively and c is the constant
a, b, and c are real numbers, and neither equal to zero
Examples of equations are:
x+3y=4
2x+7y-9 =0
A linear equation in two variables may have an infinite number of solutions, these solutions are plotted on the graph then we get a straight line.
It can say “Every point on the line is a solution to the equation and every solution to the equation is a point on the line”.
To solve a system of two linear equations, we want to find the values of the variables (x,y) that are solutions to both equations.
Types of Solution of system of Linear equation
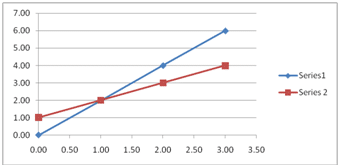
One solution
There is only one solution when given lines are intersecting each other. See below graph:
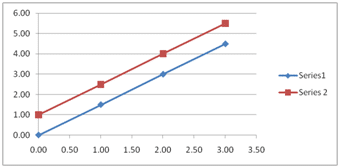
No solution
There is no solution when the given lines are parallel. See below graph:
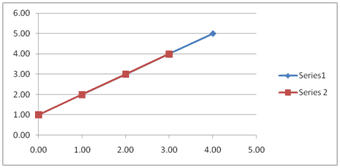
Infinite Solution
There are infinite solutions, when both lines coincide with each other.
Method of Solution of Linear Equation
The following five methods are used to solve pairs of linear equations in two variables:
- Substitution method
- Elimination method
- Graphical method
- Cross multiplication method
- Determinant method
In this article, we will solve the system of two linear equations in two variables by the first three listed methods.
The given equations are;
x+3y=4
2x+7y=9
Solution by Substitution method
The given equations are;
x+3y=4 eq. A
2x+7y=9 eq. B
Let us take equation A,
x+3y=4
⇒x=4-3y eq. C
Substitute the x value in equation B
2x+7y=9
⇒ 2(4-3y)+7y=9
⇒ 8-6y+7y=9
⇒ 8+y = 9
⇒ y=9-8
⇒ y=1
Substitute y=1 in the equation C
x=4-3(1)
⇒x=4-3
⇒x=1
Therefore, the solution of the given system is (1,1)
Solution by Elimination method
In the elimination method by adding or subtracting the two equations, we eliminate one variable from the equation. Sometimes adding or subtracting one variable directly eliminates, however mostly we multiply or divide the equation with any number, so the coefficient of one variable will become the same and during adding or subtracting the equation, it will eliminate
The given equations are;
x+3y=4 eq. A
2x+7y=9 eq. B
Multiply equation A by 2
Eq. A becomes
2x+6y=8 eq. Z
Subtracting eq.Z from eq.B
2x + 7y = 9
_2x +_6y =_8
______________
y =1
y=1 put in eq.A
x+3(1)=4
⇒ x+3=4
⇒x=4-3
⇒x=1
Therefore, the solution of the given system is (1,1)
Solution by Graphical method
To solve a system of two equations in two variables graphically, we graph each equation and the point of intersection is the solution of the given system.
The given equations are;
x+3y=4 eq. A
2x+7y=9 eq. B
Put x or y value as -2, -1,0, 1, 2, and so on, and find the corresponding values of y or x in both equations
Take eq. A
x+3y=4
⇒x=4-3y eq.C
Put y=-2 in eq.C
⇒x=4-3(-2)
x= 10
Put y=0 in eq.C
⇒x=4-3(0)
x= 4
Put y=1 in eq.C
⇒x=4-3(1)
x=1
Put y=3 in eq.C
⇒x=4-3(3)
x=-5
| X | 10 | 4 | 1 | -5 |
| Y | -2 | 0 | 1 | 3 |
Take eq. B
2x+7y=9 eq. B
⇒2x=9-7y
⇒x=(9-7y)/2 eq. D
Put y=-3 in Eq. D
⇒x=(9-7(-3))/2
⇒x=30/2
⇒x=15
Put y=-1 in Eq. D
⇒x=(9-7(-1))/2
⇒x=16/2
⇒x=8
Put y=1 in Eq. D
⇒x=(9-7(1))/2
⇒x=2/2
⇒x=1
Put y=3 in Eq. D
⇒x=(9-7(3))/2
⇒x=-12/2
⇒x=-6
| x | 15 | 8 | 1 | -6 |
| y | -3 | -1 | 1 | 3 |
Now, we will plot the graph with the help of the calculated coordinates of both equations. Find the point of intersection on the graph and then verify the solution
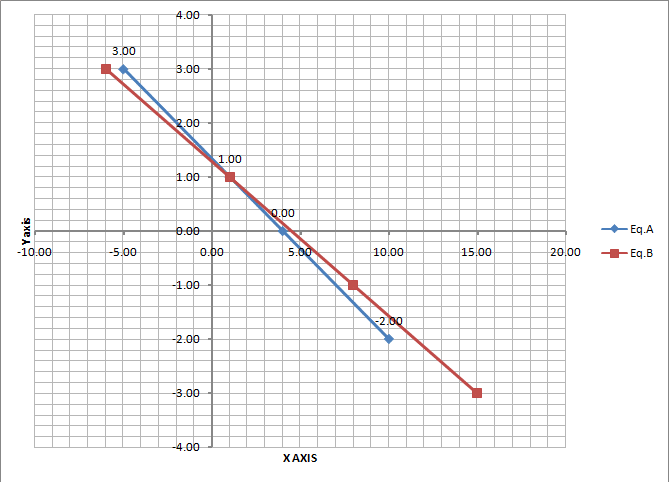
From graph we find the point of intersection (1, 1), Now we will verify the solution
Put x=1& y=1 in eq. A
x+3y=4
⇒1+3(1)=4
⇒4=4
L.H.S=R.H.S
Solution is verified, therefore, the solution of the given system is (1,1)
Note: In some cases, both lines may not intersect each other. In that case, lines are parallel and the linear equations in two variables have no solution.
You can also calculate the solution of two variables and three variables linear equation by using the below-mentioned calculator “https://knowledgesharingplatform.com/linear-equationtwo-three-variables-calculator/”

Leave a Reply