Mohr’s Circle Calculator – Principal Stresses, Max. Shear Stress, Rotation Angle & Von Mises Stress

What is Mohr’s Circle?

Mohr’s Circle is a graphical method in mechanics to find:

• Principal stresses (σ₁, σ₂)
• Maximum shear stress (τmax)
• Stress transformation at any angle

It converts complex 2D stress problems into a circle diagram for easy visualization.

How to Construct Mohr’s Circle

Suppose a material element has the following data:

• Normal stress in x-direction = σx
• Normal stress in y-direction = σy
• Shear stress = τxy

Plot the coordinates (σ, τ):

• Point A = (σx, τxy)
• Point B = (σy, –τxy)

Find the center of the circle (C)= C=σx​+σy​​ /2

Radius (R)= ((σx​-σy/2)²+(τxy)² )^1/2

Principal stresses (σ₁, σ₂): C ± R

Maximum shear stress: τmax=R

Principle plane angle =θₚ = 1/2* tan^-1(2τₓᵧ /(σₓ − σᵧ))

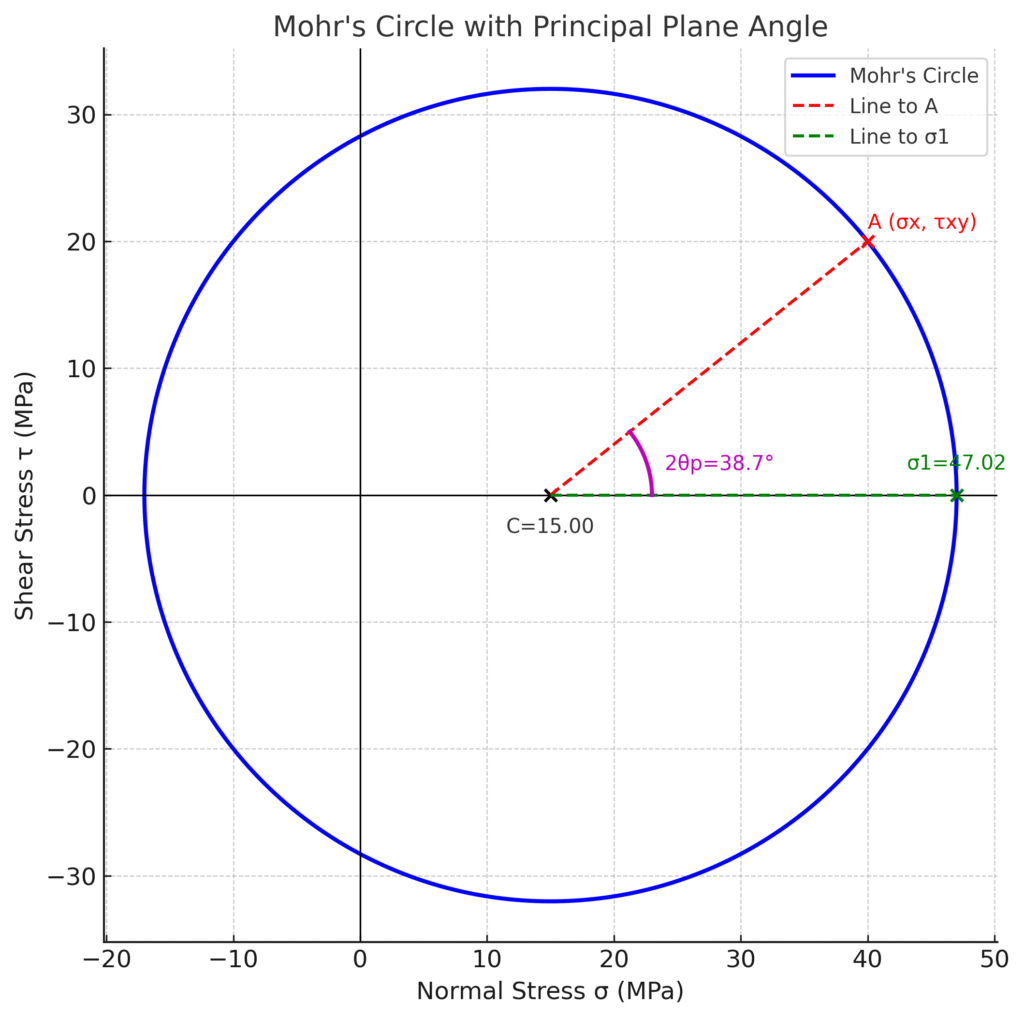
Example

σx = 40.0 MPa, σy = –10.0 MPa, τxy = 20.0 MPa

Center (C)= C=σx​+σy​​ /2 = (40-10)/2 =15 MPa

Radius (R)= ((σx​-σy/2)²+(τxy)² )^1/2 = (((40+10)/2)²+(20)² )^1/2 =32.016MPa

Principal stresses:

σ₁ = C + R = 15 + 32.016=48.016 MPa

σ₂ = C – R = 15 – 32.016= -17.016 MPa

Maximum shear stress τmax=R=32.016 MPa

Principle plane angle = θₚ = 1/2*tan^-1(2τₓᵧ /(σₓ − σᵧ))=1/2*tan-1(2*20/(40+10) =19.33 degree

Mohr’s Circle Calculator

The Mohr’s Circle Calculator is a powerful and user-friendly tool designed for civil, structural, and mechanical engineers who need quick and accurate stress analysis. By entering the in-plane normal stresses (σₓ, σᵧ) and shear stress (τₓᵧ), you can instantly calculate principal stresses, maximum shear stress, rotation angles, and Von Mises stress. The calculator also generates a clear Mohr’s Circle diagram, making it easy to visualize stress transformations and understand material behavior under different loading conditions. Whether you’re working on structural design, academic projects, or professional engineering tasks, this interactive calculator streamlines complex calculations and enhances your workflow.

Input σₓ, σᵧ, and τₓᵧ to compute and visualize Principal Stresses (σ₁, σ₂)Maximum Shear Stress (τₘₐₓ), Rotation Angle (θₚ) and Von Mises Stress (σ_VM) on Mohr’s Circle.

You May Also Like;

• Soil Gradation Calculator: Calculate Cu & Cc for Soil Classification