A Beginner’s Guide to Derivatives

What is a Derivatives?

In simple terms, a derivative measures how something changes about another thing. If you think about driving a car, your position changes as time passes. The car’s speed, how fast it’s moving at any given moment, is the derivative of your position with respect to time.

In mathematics, the derivative is the rate of change of a function. If you’re working with a function, say f(x), the derivative tells you how f(x) changes as x changes. We represent this as d/dx or f'(x), which denotes the derivative of a function with respect to x.

Key Rules for Finding Derivatives

Power Rule

The Power Rule is a quick and easy way to differentiate a term of the form xⁿ, where n is a constant

f’ (x)ⁿ = nx^n-1

Example:
If f(x) = x³, then the derivative is = f′(x)=3x²

If f(x) = x^-3, then the derivative is = f′(x)=-3x^-4 =-3/x⁴

Constant Rule

The derivative of any constant (e.g., 5, -2, 100) is always zero, because a constant doesn’t change, so its rate of change is zero.

Example:
If f(x) = 5, then the derivative is f'(x) = 0

Sum Rule

If you’re adding two functions together, simply find the derivative of each function and then add them

Example:
If f(x) = x² + 3x, then the derivative is:

f'(x) = 2x+3

Product Rule

When you multiply two functions together, the derivative is a bit more involved. You differentiate each function separately, then combine them as follows:

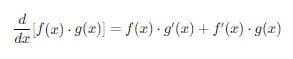
Example =F(x) = x³*sinx

Let f(x) = x³ and g(x) =sinx

first find f'(x) = 3x² and g'(x)=cosx

Then as per product rule; F'(x) = x³cosx+3x²sinx

Quotient Rule

When differentiating a function that is the quotient of two other functions, apply the Quotient Rule. This rule involves differentiating the numerator and the denominator separately, then combining them using the following formula:

Example:

F(x) = x³+1 / x²

Here f(x) = x³+1 and g(x) =x²

f'(x) = 3x² and g'(x) = 2x

Then as per quotient rule F'(x) = (x² (3x² ) – (x³+1)(2x) )/ (x²)²

F'(x) = (3x⁴ -(2x⁴ +2x) )/x⁴

F'(x) = (3x⁴ -2x⁴ -2x) / x⁴

F'(x) = (x⁴ -2x) / x⁴

F'(x) = x⁴ /x⁴ -2x /x⁴

F'(x) = 1 – 2/x³

Chain Rule

The Chain Rule is used when a function is nested inside another function, that is, when you’re dealing with a composite function like F(x)=f(g(x)

Then the derivative is F'(x) = f'(g(x)).g'(x)

Means;

• Then multiply by the derivative of the inner function.
• Differentiate the outer function, treating the inner function as a single variable.

Example

F(x) = (3x +1)²

here f(x) =3x+1 and g(x) =(f(x))²

g'(x) =2 f(x) = 2(3x+1)

f'(x) =3

therefore, F'(x) = 2(3x+1) * 3

F'(x) = 6(3x+1)

Conclusion

Derivatives might sound tricky at first, but they’re really just about figuring out how things change. Whether it’s speed, growth, or anything else that changes over time, derivatives help us understand it better. Once you learn the basic rules, like how to deal with powers, products, or chains, it all starts to make sense. With a bit of practice, using derivatives can become a useful skill in both math and real life.