This article provides a brief explanation of the slab design procedure using the moment coefficient method. Before starting the design, the structure designer completes the following tasks:
- Create a beam framing plan: Mark the location of the proposed beams on the plan and obtain approval from the Architect for the beam placement.
- Determine the slab type: Verify whether the slab is one-way or two-way by calculating the ratio of the longer span (Ly) to the shorter span (Lx).
- If Ly/Lx > 2, the slab is one-way.
- If Ly/Lx < 2, the slab is two-way.
Here:
- Ly = longer span
- Lx = shorter span
Design Procedure of One-way Slab (Ly/Lx > 2)
when Ly/Lx > 2, the slab is designed as a one-way slab. In one-way slabs, loads are distributed in the longer direction.

Minimum thickness of slab
First, determine the minimum thickness of the one-way slab. Next, ensure the slab thickness is equal to or greater than the minimum required to control deflection. Otherwise, deflection must be checked against the allowable limits. Additionally, the minimum criteria for one-way slab thickness are outlined in the table below (Refer to Table 1):
| Support condition | hmin |
| Simply supported | Lx/20 |
| One end continuous | Lx/24 |
| Two end continuous | Lx/28 |
| Cantilever | Lx/10 |
Loads on slab
- Dead load
Self wt (KN/m2) = (unit wt of material) × thickness of slab.
Finishes (KN/m2) = (unit wt of material) × finishes thickness
- Live Load
Pick up live load according to floor/ roof occupancy
Moment Calculation
- Pick up the moment coefficient according to the support condition from the below table (Refer Table 2).
| Support condition | Positive moment Coefficient | Negative moment Coefficient | |||
| Exterior span | Interior span | Exterior support | Interior support | ||
| Simply supported slab | 1/8 | 1/8 | – | – | |
| Two Span slab | 1/14 | 1/14 | 1/16 | 1/9 | |
| More then two span slab | 1/14 | 1/16 | 1/16 | 1st interior support | 2nd interior support |
| 1/10 | 1/11 | ||||
- Calculate the moment (in KN-m/m) using the formula for both (i.e., support and span) by taking the respective coefficient
Mu= coefficient × Wu × LX2
here;
Wu= Ultimate load(Factored Dead + Factored Live)
Lx = Slab shorter span
Calculation for the area of steel
- Calculate Ru (in Mpa) using the formula for each Mu(i.e., support and span moment)
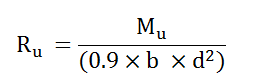
- Calculate steel ratio (ρ) using the formula below for each Ru

here;
- Calculate the Area of steel (in mm2/m) using the below formula for each ρ

- Calculate the minimum area (in mm2/m) of steel

- Compare each As with Asmin and select the greater values
- Calculate the spacing of bars (in mm) using the governing value of each As
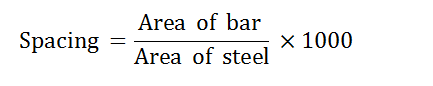
Note:
1-One-way slab calculator is available at this link, “https://knowledgesharingplatform.com/one-way-rcc-slab-design-calculator-as-per-aci-318m/“
2- Cantilever slab calculator is available at this link.”https://knowledgesharingplatform.com/cantilever-rcc-slab-design-calculator-as-per-aci-318m/“
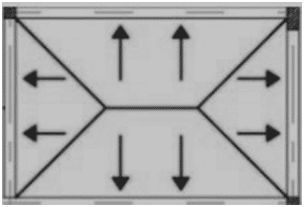
Design Procedure of Two-way Slab (Ly /Lx < 2)
If Ly/Lx < 2, the Slab is designed as a two-way slab. In two ways, slab loads are distributed in both directions.
Minimum thickness of the slab
- Calculate the minimum thickness of the slab using the formula provided below. Ensure the slab thickness is equal If Ly/Lx < 2, the Slab is designed as a two-way slab. In two ways, slab loads are distributed in both directions.to or greater than the calculated minimum to effectively control deflection. If the thickness is less, deflection must be verified against the allowable limits.
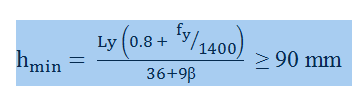
Loads on slab
- Dead load
Self wt (KN/m2) = (unit wt of material) × thickness of slab.
Finishes (KN/m2) = (unit wt of material) × finishes thickness.
- Live Load
Pick up live load according to floor/ roof occupancy
Moment Calculation
Calculate positive and negative moments (In KN-m/m) by taking the moment coefficient from the provided table below. These coefficients are based on the continuity or discontinuity of the slab in all directions.
- Positive (+ve) moment
For positive moments (i.e. span moments in both directions) dead and live load coefficients are different, which are provided in the below table (Refer Table:3):
| Ratio m = Lx/Ly | All Edges Conti-nious | One Short Edge Disco-ntinious | One Long Edge Disco-ntinio-us | Two Adjacent Edges Discon-tinious | Two Short Edges Discont-inious | Two Long Edges Discon-tinious | One Long Edge Conti-nious | One Short Edge Contin-ious | Four Edges Disco-ntinio-us | |
| 1 | CX(DL) | 0.018 | 0.023 | 0.020 | 0.027 | 0.027 | 0.018 | 0.033 | 0.027 | 0.036 |
| Cy(DL) | 0.018 | 0.020 | 0.023 | 0.027 | 0.018 | 0.027 | 0.027 | 0.033 | 0.036 | |
| Cx(LL) | 0.027 | 0.030 | 0.028 | 0.032 | 0.032 | 0.027 | 0.035 | 0.032 | 0.036 | |
| Cy(LL) | 0.027 | 0.028 | 0.030 | 0.032 | 0.027 | 0.032 | 0.032 | 0.035 | 0.036 | |
| 0.95 | CX(DL) | 0.020 | 0.024 | 0.022 | 0.030 | 0.028 | 0.021 | 0.036 | 0.031 | 0.040 |
| Cy(DL) | 0.016 | 0.017 | 0.021 | 0.024 | 0.015 | 0.025 | 0.024 | 0.031 | 0.033 | |
| Cx(LL) | 0.030 | 0.032 | 0.031 | 0.035 | 0.034 | 0.031 | 0.038 | 0.036 | 0.040 | |
| Cy(LL) | 0.025 | 0.025 | 0.027 | 0.029 | 0.024 | 0.029 | 0.029 | 0.032 | 0.033 | |
| 0.9 | CX(DL) | 0.022 | 0.026 | 0.025 | 0.033 | 0.029 | 0.025 | 0.039 | 0.035 | 0.045 |
| Cy(DL) | 0.014 | 0.015 | 0.019 | 0.022 | 0.013 | 0.024 | 0.021 | 0.028 | 0.029 | |
| Cx(LL) | 0.034 | 0.036 | 0.035 | 0.039 | 0.037 | 0.035 | 0.042 | 0.040 | 0.045 | |
| Cy(LL) | 0.022 | 0.022 | 0.024 | 0.026 | 0.021 | 0.027 | 0.025 | 0.029 | 0.029 | |
| 0.85 | CX(DL) | 0.024 | 0.028 | 0.029 | 0.036 | 0.031 | 0.029 | 0.042 | 0.040 | 0.050 |
| Cy(DL) | 0.012 | 0.013 | 0.017 | 0.019 | 0.011 | 0.022 | 0.017 | 0.025 | 0.026 | |
| Cx(LL) | 0.037 | 0.039 | 0.040 | 0.043 | 0.041 | 0.040 | 0.046 | 0.045 | 0.050 | |
| Cy(LL) | 0.019 | 0.020 | 0.022 | 0.023 | 0.019 | 0.024 | 0.022 | 0.026 | 0.026 | |
| 0.8 | CX(DL) | 0.026 | 0.029 | 0.032 | 0.039 | 0.032 | 0.034 | 0.045 | 0.045 | 0.056 |
| Cy(DL) | 0.011 | 0.010 | 0.015 | 0.016 | 0.009 | 0.020 | 0.015 | 0.022 | 0.023 | |
| Cx(LL) | 0.041 | 0.042 | 0.044 | 0.048 | 0.044 | 0.045 | 0.051 | 0.051 | 0.056 | |
| Cy(LL) | 0.017 | 0.017 | 0.019 | 0.020 | 0.016 | 0.022 | 0.019 | 0.023 | 0.023 | |
| 0.75 | CX(DL) | 0.028 | 0.031 | 0.036 | 0.043 | 0.033 | 0.040 | 0.048 | 0.051 | 0.061 |
| Cy(DL) | 0.009 | 0.007 | 0.013 | 0.013 | 0.007 | 0.018 | 0.012 | 0.020 | 0.019 | |
| Cx(LL) | 0.045 | 0.046 | 0.049 | 0.052 | 0.047 | 0.051 | 0.055 | 0.056 | 0.061 | |
| Cy(LL) | 0.014 | 0.013 | 0.016 | 0.016 | 0.013 | 0.019 | 0.016 | 0.020 | 0.019 | |
| 0.7 | CX(DL) | 0.030 | 0.033 | 0.040 | 0.046 | 0.035 | 0.046 | 0.051 | 0.058 | 0.068 |
| Cy(DL) | 0.007 | 0.006 | 0.011 | 0.011 | 0.005 | 0.016 | 0.009 | 0.017 | 0.016 | |
| Cx(LL) | 0.049 | 0.050 | 0.054 | 0.057 | 0.051 | 0.057 | 0.060 | 0.063 | 0.068 | |
| Cy(LL) | 0.012 | 0.011 | 0.014 | 0.014 | 0.011 | 0.016 | 0.013 | 0.017 | 0.016 | |
| 0.65 | CX(DL) | 0.032 | 0.034 | 0.044 | 0.050 | 0.036 | 0.054 | 0.054 | 0.065 | 0.074 |
| Cy(DL) | 0.006 | 0.005 | 0.009 | 0.009 | 0.004 | 0.014 | 0.007 | 0.014 | 0.013 | |
| Cx(LL) | 0.053 | 0.054 | 0.059 | 0.062 | 0.055 | 0.064 | 0.064 | 0.070 | 0.074 | |
| Cy(LL) | 0.010 | 0.009 | 0.011 | 0.011 | 0.009 | 0.014 | 0.010 | 0.014 | 0.013 | |
| 0.6 | CX(DL) | 0.034 | 0.036 | 0.048 | 0.053 | 0.037 | 0.062 | 0.056 | 0.073 | 0.081 |
| Cy(DL) | 0.004 | 0.004 | 0.007 | 0.007 | 0.003 | 0.011 | 0.006 | 0.012 | 0.010 | |
| Cx(LL) | 0.058 | 0.059 | 0.065 | 0.067 | 0.059 | 0.071 | 0.068 | 0.077 | 0.081 | |
| Cy(LL) | 0.007 | 0.007 | 0.009 | 0.009 | 0.007 | 0.011 | 0.008 | 0.011 | 0.010 | |
| 0.55 | CX(DL) | 0.035 | 0.037 | 0.052 | 0.056 | 0.038 | 0.071 | 0.058 | 0.081 | 0.088 |
| Cy(DL) | 0.003 | 0.003 | 0.005 | 0.005 | 0.002 | 0.009 | 0.004 | 0.009 | 0.008 | |
| Cx(LL) | 0.062 | 0.063 | 0.070 | 0.072 | 0.063 | 0.080 | 0.073 | 0.085 | 0.088 | |
| Cy(LL) | 0.006 | 0.006 | 0.007 | 0.007 | 0.005 | 0.009 | 0.006 | 0.009 | 0.008 | |
| 0.5 | CX(DL) | 0.037 | 0.038 | 0.056 | 0.059 | 0.039 | 0.080 | 0.061 | 0.089 | 0.095 |
| Cy(DL) | 0.002 | 0.002 | 0.004 | 0.004 | 0.001 | 0.007 | 0.003 | 0.007 | 0.006 | |
| Cx(LL) | 0.066 | 0.067 | 0.076 | 0.077 | 0.067 | 0.088 | 0.078 | 0.092 | 0.095 | |
| Cy(LL) | 0.004 | 0.004 | 0.005 | 0.005 | 0.004 | 0.007 | 0.005 | 0.007 | 0.006 | |
Moments in both directions are calculated using the below formulas:
For the Main bar parallel to the shorter direction
Mu1 (+ve) = (CX(DL)× Wu(DL) × LX2 )+ (CX(LL)× Wu(LL) × Lx2 )
For the Main bar parallel to the longer direction
Mu2 (+ve) = (Cy(DL)× Wu(DL) × Ly2 )+ (Cy(LL)× Wu(LL) × Ly2 )
Negative(-ve) moment
Negative moment coefficients are the same for dead and live, which are provided in the below table (Refer Table: 4)
| Ratio m = Lx/Ly | All Edges Contini-ous | One Short Edge Discont-inious | One Long Edge Discont-inious | Two Adjacent Edges Discont-inious | Two Short Edges Disco-ntinio-us | Two Long Edges Disco-ntinio-us | One Long Edge Conti-nious | One Short Edge Conti-nious | Four Edges Disco-ntinio-us | |
| 1 | Cx(DL+LL) | 0.045 | 0.061 | 0.033 | 0.050 | 0.075 | 0.071 | |||
| Cy(DL+LL) | 0.045 | 0.033 | 0.061 | 0.050 | 0.076 | 0.071 | ||||
| 0.95 | Cx(DL+LL) | 0.050 | 0.065 | 0.038 | 0.055 | 0.079 | 0.075 | |||
| Cy(DL+LL) | 0.041 | 0.029 | 0.056 | 0.045 | 0.072 | 0.067 | ||||
| 0.9 | Cx(DL+LL) | 0.055 | 0.068 | 0.043 | 0.060 | 0.080 | 0.079 | |||
| Cy(DL+LL) | 0.037 | 0.025 | 0.052 | 0.040 | 0.070 | 0.062 | ||||
| 0.85 | Cx(DL+LL) | 0.060 | 0.072 | 0.049 | 0.066 | 0.082 | 0.083 | |||
| Cy(DL+LL) | 0.031 | 0.021 | 0.046 | 0.034 | 0.065 | 0.057 | ||||
| 0.8 | Cx(DL+LL) | 0.065 | 0.075 | 0.055 | 0.071 | 0.083 | 0.086 | |||
| Cy(DL+LL) | 0.027 | 0.017 | 0.041 | 0.029 | 0.061 | 0.051 | ||||
| 0.75 | Cx(DL+LL) | 0.069 | 0.078 | 0.061 | 0.076 | 0.085 | 0.088 | |||
| Cy(DL+LL) | 0.022 | 0.014 | 0.036 | 0.024 | 0.056 | 0.044 | ||||
| 0.7 | Cx(DL+LL) | 0.074 | 0.081 | 0.068 | 0.081 | 0.086 | 0.091 | |||
| Cy(DL+LL) | 0.017 | 0.011 | 0.029 | 0.019 | 0.050 | 0.038 | ||||
| 0.65 | Cx(DL+LL) | 0.077 | 0.083 | 0.074 | 0.085 | 0.087 | 0.093 | |||
| Cy(DL+LL) | 0.014 | 0.008 | 0.024 | 0.015 | 0.043 | 0.031 | ||||
| 0.6 | Cx(DL+LL) | 0.081 | 0.085 | 0.080 | 0.089 | 0.088 | 0.095 | |||
| Cy(DL+LL) | 0.010 | 0.006 | 0.018 | 0.011 | 0.035 | 0.024 | ||||
| 0.55 | Cx(DL+LL) | 0.084 | 0.086 | 0.085 | 0.092 | 0.089 | 0.096 | |||
| Cy(DL+LL) | 0.007 | 0.005 | 0.014 | 0.008 | 0.028 | 0.019 | ||||
| 0.5 | Cx(DL+LL) | 0.086 | 0.088 | 0.089 | 0.094 | 0.090 | 0.097 | |||
| Cy(DL+LL) | 0.006 | 0.003 | 0.010 | 0.006 | 0.022 | 0.014 | ||||
Calculation for the area of steel
- Calculate Ru (in Mpa) for all positive and negative moments using the below formula:
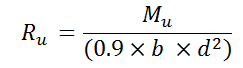
- Calculate steel ratio (ρ) using the below formula for each Ru
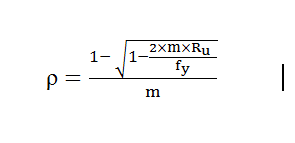
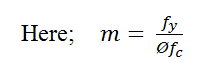
- Calculate the Area of steel (in mm2/m) using the below formula for each ρ
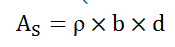
- Calculate the minimum area (in mm2/m) of steel.
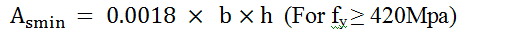
- Compare As with Asmin and select the greater value
- Calculate the spacing of bars (in mm) using the governing value of each As

Note: The two-way slab Design calculator is provided at this link, “https://knowledgesharingplatform.com/two-way-rcc-slab-design-calculator-as-per-aci-318m/“
References
- All formulas are from “ACI 318 code”.
- Moment coefficients for two-way slabs are taken from the book “Design of concrete structures by Winter/Nilson”.
Related Posts
Check out these related resources to dive deeper into RCC slab design.
- Cantilever RCC Slab Design Calculator as per ACI 318M
- One-Way RCC Slab Design Calculator as per ACI 318M
- Two-Way RCC Slab Design Calculator as per ACI 318M
- Load Distribution from Slab to Beam
- Slab Reinforcement Calculator Based on Unit Strip Moment

Leave a Reply