A quadratic equation is an equation of degree 2, meaning that the highest exponent of the variable is 2. In its standard form, the quadratic equation is written as ax²+bx+c where a ≠ 0.

 In this equation, xxx represents an unknown value, while aaa, bbb, and ccc are the coefficients of the equation.

There are several methods to solve a quadratic equation. However, among all these methods, the most universally applicable and reliable approach is the solution of quadratic equation using quadratic formula. Therefore, in this article, we will focus on understanding the solution of quadratic equation using quadratic formula step by step.

Quadratic Formula`

The quadratic formula is a powerful tool for solving quadratic equations of the form ax²+bx+c =0. It states that the solution for x can be found using the below-mentioned formula:

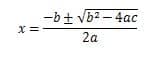
Nature of Roots of Quadratic Equation

The nature of the solutions of a quadratic equation depends on the discriminant (i.e. b²-4ac) of the equation. The discriminant determines whether the solutions are real, repeated, or complex. The following are the possible cases:

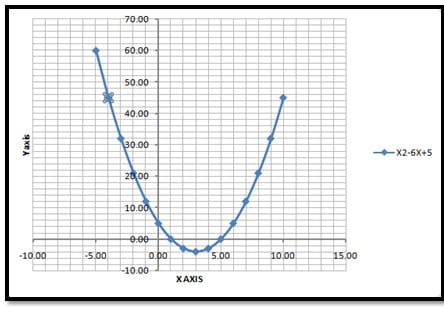
1. Discriminant, b²-4ac > 0, it indicates that the quadratic equation has two distinct real solutions, which means the graph of the quadratic equation intersects the x-axis at two distinct points. The example is shown below;

Take Equation x²-6x+5=0

Here;

a = 1, b=-6, c = 5

Calculate Descriminant

⇒ b²-4ac

⇒ (-6)²-4(1)(5)

⇒36-20 = 16> 0 means roots have two distinct solution

Plot the graph of the taken equation, it is also clear from the graph that the curve intersects X axis at two distinct points. See below graph

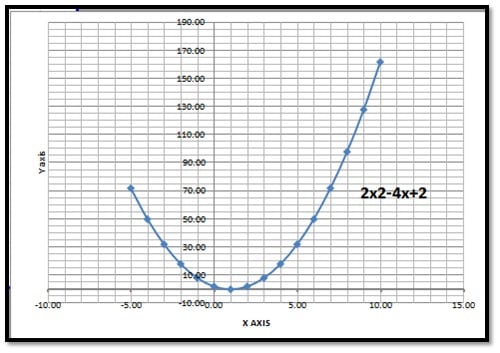
2. Discriminant, b²-4ac = 0, it indicates that the quadratic equation has one real solution: a repeated root. Geometrically, this means the graph of the quadratic equation touches the x-axis at one point. Example is given below;

Take Equation 2x²-4x+2=0

Here;

a = 2, b=-4, c = 2

Calculate Descriminant = b²-4ac

⇒ (-4)²-4(2)(2)

⇒16-16 = 0 = 0 means roots have only one solution

Plot the graph of the taken equation, it is also clear from the graph that curve intersects X axis at only one point. See below graph

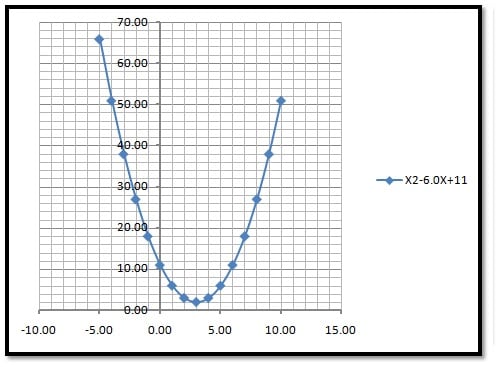
3. Discriminant, b²-4ac < 0, it indicates that the quadratic equation has two complex solutions. These solutions are not real numbers but involve the imaginary unit i. Geometrically, this means the graph of the quadratic equation does not intersect the x-axis.

Take Equation x²-6x +11=0

Here;

a = 1, b=-6, c = 11

Calculate Descriminant

⇒ b²-4ac

⇒ (-6)²-4(1)(11)

⇒ 36-44 = -8 < 0 means roots have two complex solution

Plot the graph of the taken equation, it is also clear from the graph that the curve does not intersect the X-axis. See below graph

Solutions of Quadratic Equation

Now we will solve quadratic equations using the “Quadratic formula”. A step-by-step method and examples are listed below:

1. Write the quadratic equation in the form of ax²+bx+c =0
2. Identify the coefficients a, b, and c in the quadratic equation
3. Substitute the values of a, b, and c into the quadratic formula and determine the solutions for x

 Examples 1; Two Distinct Real Solution

Examples 2; One Real Solution

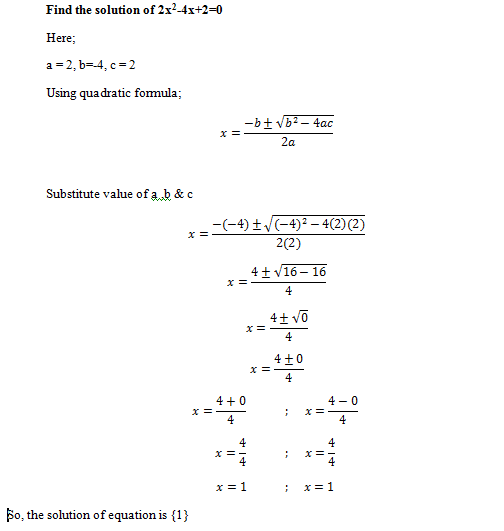
Examples 3; Two Complex Solution

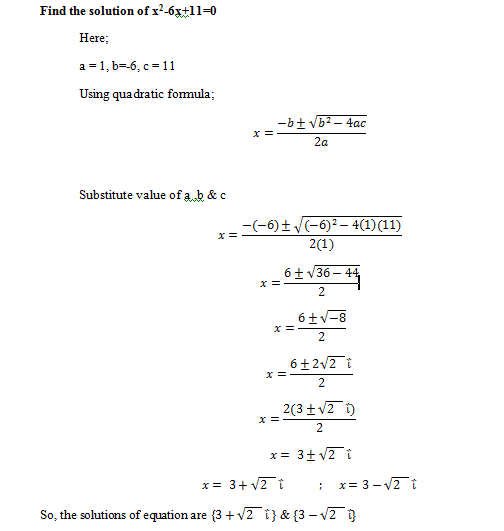
Conclusion

The quadratic formula is a simple yet highly effective method for solving quadratic equations. It is especially useful because it can be applied to all possible types of roots—real or complex—making it a more suitable and versatile approach compared to other methods.

Note: you can calculate quadratic roots by using below calculator; “https://knowledgesharingplatform.com/quadratic-equations-solver/“